Where Mathematics Comes From

Where Mathematics Comes From: How the Embodied Mind Brings Mathematics into Being (hereinafter WMCF) is a book by George Lakoff, a cognitive linguist, and Rafael E. Núñez, a psychologist. Published in 2000, WMCF seeks to found a cognitive science of mathematics, a theory of embodied mathematics based on conceptual metaphor.

Contents

WMCF definition of mathematics

Mathematics makes up that part of the human conceptual system that is special in the following way:

"It is precise, consistent, stable across time and human communities, symbolizable, calculable, generalizable, universally available, consistent within each of its subject matters, and effective as a general tool for description, explanation, and prediction in a vast number of everyday activities, [ranging from] sports, to building, business, technology, and science." (WMCF, pp. 50, 377)

Nikolay Lobachevsky said "There is no branch of mathematics, however abstract, which may not some day be applied to phenomena of the real world." A common type of conceptual blending process would seem apply to the entire mathematical procession. Pythagoras said "All is number."

Human cognition and mathematics

Lakoff and Núñez's avowed purpose is to begin laying the foundations for a truly scientific understanding of mathematics, one grounded in processes common to all human cognition. They find that four distinct but related processes metaphorically structure basic arithmetic: object collection, object construction, using a measuring stick, and moving along a path.

WMCF builds on earlier books by Lakoff (1987) and Lakoff and Johnson (1980, 1999), which analyze such concepts of metaphor and image schemata from second-generation cognitive science. Some of the riches of these earlier books, such as the interesting technical ideas in Lakoff (1987), are absent from WMCF.

Lakoff and Núñez hold that mathematics results from the human cognitive apparatus and must therefore be understood in cognitive terms. WMCF advocates (and includes some examples of) a cognitive idea analysis of mathematics which analyzes mathematical ideas in terms of the human experiences, metaphors, generalizations, and other cognitive mechanisms giving rise to them. A standard mathematical education does not develop such idea analysis techniques because it does not pursue considerations of A) what structures of the mind allow it to do mathematics or B) the philosophy of mathematics.

Lakoff and Núñez start by reviewing the psychological literature, concluding that human beings appear to have an innate ability, called subitizing, to count, add, and subtract up to about 4 or 5. They document this conclusion by reviewing the literature, published in recent decades, describing experiments with infant subjects. For example, infants quickly become excited or curious when presented with "impossible" situations, such as having three toys appear when only two were initially present.

The authors argue that mathematics goes far beyond this very elementary level due to a large number of metaphorical constructions. For example, they argue that the Pythagorean position that all is number, and the associated crisis of confidence that came about with the discovery of the irrationality of the square root of two, arises solely from a metaphorical relation between the length of the diagonal of a square, and the possible numbers of objects.

Much of WMCF deals with the important concepts of infinity and of limit processes, seeking to explain how finite humans living in a finite world could ultimately conceive of the actual infinite. Thus much of WMCF is, in effect, a study of the epistemological foundations of the calculus. Lakoff and Núñez conclude that while the potential infinite is not metaphorical, the actual infinite is. Moreover, they deem all manifestations of actual infinity to be instances of what they call the "Basic Metaphor of Infinity", as represented by the ever-increasing sequence 1, 2, 3, ...

WMCF emphatically rejects the Platonistic philosophy of mathematics. They emphasize that all we know and can ever know is human mathematics, the mathematics arising from the human intellect. The question of whether there is a "transcendent" mathematics independent of human thought is a meaningless question. That is like asking if colors are transcendent of human thought- colors are only varying wavelengths of light, it is our interpretation of physical stimuli that make them colors.

WMCF (p. 81) likewise criticizes the emphasis mathematicians place on the concept of closure. Lakoff and Núñez argue that the expectation of closure is an artifact of the human mind's ability to relate fundamentally different concepts via metaphor.

WMCF concerns itself mainly with proposing and establishing an alternative view of mathematics, one grounding the field in the realities of human biology and experience. It is not a work of technical mathematics or philosophy. Lakoff and Núñez are not the first to argue that conventional approaches to the philosophy of mathematics are flawed. For example, they do not seem all that familiar with the content of Davis and Hersh (1981), even though WMCF warmly acknowledges Reuben Hersh's support.

Lakoff and Núñez cite Saunders MacLane (the inventor, with Samuel Eilenberg, of category theory) in support of their position. MacLane (1986), an overview of mathematics intended for philosophers, proposes that mathematical concepts are ultimately grounded in ordinary human activities, mostly interactions with the physical world.[1] See From Action to Mathematics per Mac Lane.

Educators have taken some interest in what WMCF suggests about how mathematics is learned, and why students find some elementary concepts more difficult than others.

Examples of mathematical metaphors

Conceptual metaphors described in WMCF, in addition to the Basic Metaphor of Infinity, include:

Mathematical reasoning requires variables ranging over some universe of discourse, so that we can reason about generalities rather than merely about particulars. WMCF argues that reasoning with such variables implicitly relies on what it terms the Fundamental Metonymy of Algebra.

Example of metaphorical ambiguity

WMCF (p. 151) includes the following example of what the authors term "metaphorical ambiguity." Take the set 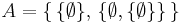A = \{ \,\{\emptyset\}, \, \{ \emptyset, \{\emptyset\}\}\,\}. Then recall two bits of standard terminology from elementary set theory:

  1. The recursive construction of the ordinal natural numbers, whereby 0 is 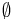\empty, and n+1 is n 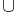\cup {n}.
  2. The ordered pair (a,b), defined as \{\, \{a\}, \{a,b\}\,\}.

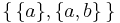By (1), A is the set {1,2}. But (1) and (2) together say that A is also the ordered pair (0,1). Both statements cannot be correct; the ordered pair (0,1) and the unordered pair {1,2} are fully distinct concepts. Lakoff and Johnson (1999) term this situation "metaphorically ambiguous." This simple example calls into question any Platonistic foundations for mathematics.

While (1) and (2) above are admittedly canonical, especially within the consensus set theory known as the Zermelo–Fraenkel axiomatization, WMCF does not let on that they are but one of several definitions that have been proposed since the dawning of set theory. For example, Frege, Principia Mathematica, and New Foundations (a body of axiomatic set theory begun by Quine in 1937) define cardinals and ordinals as equivalence classes under the relations of equinumerosity and similarity, so that this conundrum does not arise. In Quinian set theory, A is simply an instance of the number 2. For technical reasons, defining the ordered pair as in (2) above is awkward in Quinian set theory. Two solutions have been proposed:

Criticism

In set theories such as Zermelo–Fraenkel one can indeed have {1,2} = (0,1), as these are two different symbols denoting the same object. The claim that there is an anomaly because these are "fully distinct concepts" is on the one hand not a clear scientific statement, and on the other hand, is on par with such statements as: ""The positive real solution of 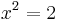x^2=2" and "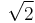\sqrt{2}" cannot be equal because they are fully distinct concepts.".

The apparent anomaly stems from the fact that Lakoff and Núñez identify mathematical objects with their various particular realizations. There are several equivalent definitions of ordered pair, and most mathematicians do not identify the ordered pair with just one of these definitions (since this would be an arbitrary and artificial choice), but view the definitions as equivalent models or realizations of the same underlying object. The existence of several different but equivalent constructions of certain mathematical objects supports the platonistic view that the mathematical objects exist beyond their various linguistical, symbolical, or conceptual representations.

As an example, many mathematicians would favour a definition of ordered pair in terms of category theory where the object in question is defined in terms of a characteristic universal property and then shown to be unique up to unique isomorphism (this was recently mentioned in an article on mathematical platonism by David Mumford).

The above discussion is meant to explain that the most natural and fruitful approach in mathematics is to view a mathematical object as having potentially several different but equivalent realizations. On the other hand, the object is not identified with just one of these realizations. This suggests that the intuitionistic idea that mathematical objects exist only as specific mental constructions, or the idea of Lakoff and Núñez that mathematical objects exist only as particular instances of concepts/metaphors in our embodied brains, is an inadequate philosophical basis to account for the experience and de facto research methods of working mathematicians. Perhaps this is a reason why these ideas have been met with comparatively little interest by the mathematical community.

The Romance of Mathematics

The "Romance of Mathematics" is WMCF's light-hearted term for a perennial philosophical viewpoint about mathematics the authors describe, then dismiss as an intellectual myth:

It is very much an open question whether WMCF will eventually prove to be the start of a new school in the philosophy of mathematics. Hence the main value of WMCF so far may be a critical one: its critique of Platonism in mathematics, and the Romance of Mathematics.

Critical response

Many working mathematicians resist the approach and conclusions of Lakoff and Núñez. Reviews by mathematicians of WMCF in professional journals, while often respectful of its focus on conceptual strategies and metaphors as paths for understanding mathematics, have taken exception to some of the WMCF's philosophical arguments on the grounds that mathematical statements have lasting 'objective' meanings. For example, Fermat's last theorem means exactly what it meant when Fermat initially proposed it 1664. Other reviewers have pointed out that multiple conceptual strategies can be employed in connection with the same mathematically defined term, often by the same person (a point that is compatible with the view that we routinely understand the 'same' concept with different metaphors). The metaphor and the conceptual strategy are not the same as the formal definition which mathematicians employ. However, WMCF points out that formal definitions are built using words and symbols that have meaning only in terms of human experience.

Critiques of WMCF include the humorous:

"It's difficult for me to conceive of a metaphor for a real number raised to a complex power, but if there is one, I'd sure like to see it." - Joseph Auslander[2]

and the physically informed:

"But their analysis leaves at least a couple of questions insufficiently answered. For one thing, the authors ignore the fact that brains not only observe nature, but also are part of nature. Perhaps the math that brains invent takes the form it does because math had a hand in forming the brains in the first place (through the operation of natural laws in constraining the evolution of life). Furthermore, it's one thing to fit equations to aspects of reality that are already known. It's something else for that math to tell of phenomena never previously suspected. When Paul Dirac's equations describing electrons produced more than one solution, he surmised that nature must possess other particles, now known as antimatter. But scientists did not discover such particles until after Dirac's math told him they must exist. If math is a human invention, nature seems to know what was going to be invented."[2]

Mathematicians have also complained that Lakoff and Núñez have misunderstood some basic mathematical notions. The authors reply that the errors found in earlier printings of WMCF are now corrected.

Lakoff made his reputation by linking linguistics to cognitive science and the analysis of metaphor. Núñez, educated in Switzerland, is a product of Jean Piaget's school of cognitive psychology as a basis for logic and mathematics. Núñez has thought much about the foundations of real analysis, the real and complex numbers, and the Basic Metaphor of Infinity. These topics, however, worthy though they be, form part of the superstructure of mathematics. Cognitive science should take more interest in the foundations of mathematics. And indeed, the authors do pay a fair bit of attention early on to logic, Boolean algebra and the Zermelo–Fraenkel axioms, even lingering a bit over group theory. But neither author is well-trained in logic (there is no index entry for "quantifier" or "quantification"), the philosophy of set theory, the axiomatic method, metamathematics, and model theory. Nor does WMCF say enough about the derivation of number systems (the Peano axioms go unmentioned), abstract algebra, equivalence and order relations, mereology, topology, and geometry.

Lakoff and Núñez tend to dismiss the negative opinions mathematicians have expressed about WMCF, because their critics do not appreciate the insights of cognitive science. Lakoff and Núñez maintain that their argument can only be understood using the discoveries of recent decades about the way human brains process language and meaning. They argue that any arguments or criticisms that are not grounded in this understanding cannot address the content of the book.[3]

It has been pointed out that it is not at all clear that WMCF establishes that the claim "intelligent alien life would have mathematical ability" is a myth. To do this, it would be required to show that intelligence and mathematical ability are separable, and this has not been done. On Earth, intelligence and mathematical ability seem to go hand in hand in all life-forms, as pointed out by Keith Devlin among others. The authors of WMCF have not explained how this situation would (or even could) be different anywhere else.

Lakoff and Núñez also appear not to appreciate the extent to which intuitionists and constructivists have anticipated their attack on the Romance of (Platonic) Mathematics. Brouwer, the founder of the intuitionist/constructivist point of view, wrote "Mathematics is a free construction of the human mind." Hence at least one person writing before Lakoff and Núñez were born concluded that mathematics emerged to serve human purposes and has no existence apart from this fact.

Summing up

WMCF (pp. 378–79) concludes with some key points, a number of which follow. Mathematics arises from our bodies and brains, our everyday experiences, and the concerns of human societies and cultures. It is:

The cognitive approach to formal systems, as described and implemented in WMCF, need not be confined to mathematics, but should also prove fruitful when applied to formal logic, and to formal philosophy such as Edward Zalta's theory of abstract objects. Lakoff and Johnson (1999) fruitfully employ the cognitive approach to rethink a good deal of the philosophy of mind, epistemology, metaphysics, and the history of ideas.

Footnotes

  1. ^ See especially the table in Mac Lane (1986), p. 35.
  2. ^ a b What is the Nature of Mathematics?, Michael Sutcliffe, referenced February 1, 2011
  3. ^ See http://www.unifr.ch/perso/nunezr/warning.html

See also

References

External links